Propriétés techniques d'un ressort plat
LA MATIERE EST ELASTIQUE
Sous l’action d’une force, tout corps solide s’allonge, se comprime, … dans certaines limites d’extension, de compression, …, mais reprend sa forme d’origine une fois que la force a cessé d’agir :
c’est l’élasticité.
Cette propriété physique (de la matière) a été observée par le physicien Robert Hooke (1635-1703) qui a constaté la proportionnalité entre la contrainte de traction appliquée à un matériau et la déformation qui en résulte.
Par la suite, le physicien Thomas Young (1773-1829) a remarqué que le rapport entre la contrainte appliquée et la déformation produite est constant, tant que cette déformation reste inférieure à la limite d’élasticité du matériau.
Il en a découlé la loi d’élasticité, ou loi de Hooke :
σ = la contrainte, c’est-à-dire la force divisée par la section sur laquelle s’applique cette force (en unité de pression, généralement pascals ou N/m²).
E = le module de Young, ou module d’élasticité (également en unité de pression).
ε = la déformation, ou allongement relatif (sans dimension), qui correspond au rapport de l’allongement sur la longueur initiale du corps déformé.
RESISTANCE DES MATERIAUX
La Résistance des matériaux (RDM) est une discipline de la mécanique qui permet l’étude des contraintes et des déformations.
Elle est utilisée pour dimensionner des structures afin de garantir leur résistance lorsqu’elles seront soumises à des actions extérieures
Exemples : un pont supportant le poids des véhicules, un crochet soulevant une charge…
Ces actions sont principalement de deux types : les forces et les moments.
Une force appliquée en un point d’un solide aura tendance à créer un mouvement de translation, tandis qu’un moment aura tendance à mettre un solide en mouvement de rotation.
Un outil mathématique appelé torseur permet d’exprimer les actions mécaniques externes appliquées à un solide. Ainsi, un solide auquel on applique une force et un moment
(en un point A, dans un repère cartésien $(x↖{→},y↖{→},z↖{→})$) s'écrira :
En RDM, sous certaines hypothèses simplificatrices*, on étudie le comportement d’élément mécaniques simples nommés poutres.
Une poutre est un objet de grande longueur par rapport à sa section, chargée dans son plan moyen de symétrie, et de section droite.
A partir des efforts externes appliqués à l’élément, on détermine les efforts internes qui se produisent dans la matière.
Pour cela, on exprime le torseur des efforts internes :
avec
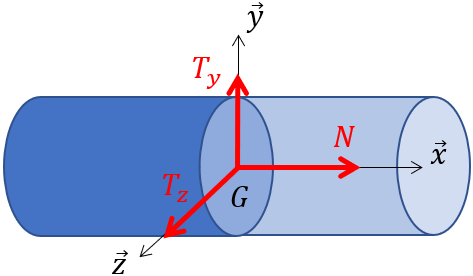
$N_x$ l’effort normal selon $x↖{→}$ (>0 si traction, <0 si compression)
$T_y$ l’effort tranchant selon $y↖{→}$
$T_z$ l’effort tranchant selon $z↖{→}$
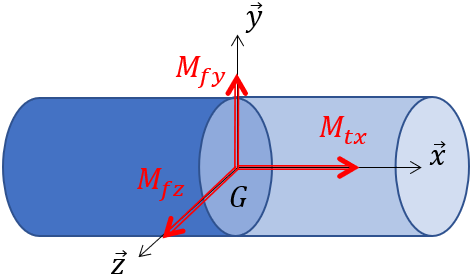
$M_{fx}$ le moment de torsion autour de $x↖{→}$
$M_{fy}$ le moment de flexion autour de $y↖{→}$
$M_{fz}$ le moment de flexion autour de $z↖{→}$
*principe de Saint-Venant, principe de Navier-Bernoulli, petites déformations, matériau continu-homogène-isotrope, élasticité linéaire, …
CAS PRATIQUE
En prenant le cas simple d’une poutre encastrée à un extrémité et libre à l’autre extrémité, à laquelle on applique un effort,
on peut exprimer les relations suivantes :
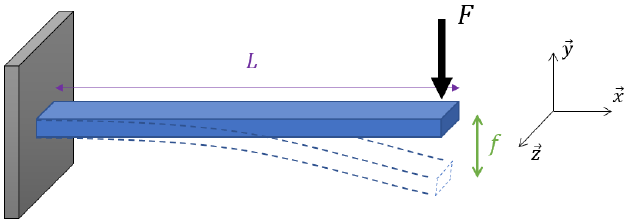
Tenseur des efforts internes :
Contrainte : Si on isole une section de la poutre, on constate que la partie supérieure travaille en traction tandis que la partie inférieure travaille en compression
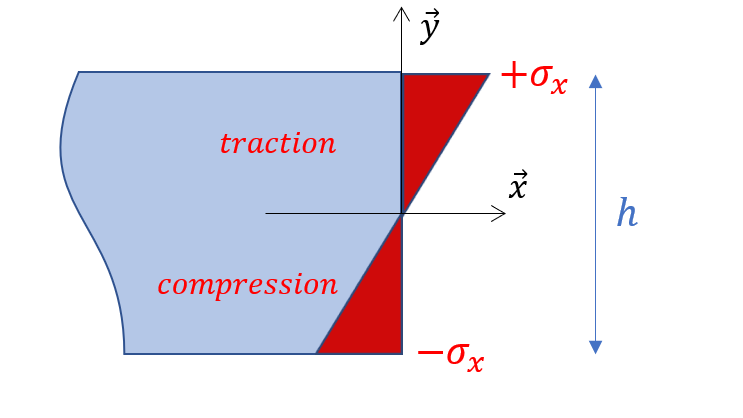
La contrainte dans cette section vaut :
On note alors une zone de transition où les contraintes sont nulles : il s’agit de la fibre neutre
(définition : ligne passant par le centre de gravité des sections droites; en petites déformations, la longueur de cette fibre ne varie pas en flexion)
Flèche : Il s’agit de la valeur maximale du déplacement de la poutre
Ces relations font intervenir un paramètre important dénommé moment quadratique $I_{Gz}$ , qui correspond à l’inertie de la section par rapport à l’axe du moment de flexion.
Dans cet exemple, pour une poutre de section rectangulaire $b ✕ h$, le moment quadratique
Selon $z$ vaut :
Et selon y :
Ce paramètre traduit le fait que pour une même section donnée, la poutre n’opposera pas la même résistance à la flexion selon son orientation.

On notera que plus le moment quadratique est grand (plus la matière est éloignée de la fibre neutre), plus la contrainte dans la poutre est petite.
L’expression de la flèche fait également apparaître la raideur de la poutre.
En effet, la raideur, généralement notée k , exprime la relation de proportionnalité entre la force F appliquée et la déflexion f qui en résulte :
qui vaut dans cet exemple $k = {3El_{Gz}}/{L^3}$
Un ressort plat fonctionne selon ces principes.
ne pas confondre
Rigidité & résistance
la résistance mécanique d’un matériau est caractérisée par sa limite d’élasticité et/ou sa résistance à la traction
Rigidité & raideur
la raideur d’une poutre dépend de son module de Young (de sa rigidité) mais aussi du rapport de sa section à sa longueur.
Rigidité & dureté
la dureté d’un matériau définit la résistance relative qu’oppose sa surface à la pénétration d’un corps plus dur.
